A Level Physics Explained - Equations of Motion

Defining Motion

· Displacement, s (m) is the vector equivalent of distance – it is distance moved in a certain direction

· v = velocity (ms-1)
s = displacement (m)
t = time (s)

Velocity, v (ms^-1) is the vector equivalent of speed – it is the speed in a given direction

· This is instantaneous velocity v = velocity (ms-1)
_s = change in displacement (m)
_t = change in time (s)

Another way of describing this is to think of velocity as the rate of change of displacement:

· a = acceleration (ms-2)
v = final velocity (ms-1)
u = initial velocity (ms-1)
t = time (s)

The rate of change of velocity is called acceleration – this is also a vector:

· This equation assumes that acceleration is constant or uniform

Equations of Motion (suvat)

· Problem solving strategy
1. Write a list of all the quantities in order;
s =
u =
v =
a =
t =

2. Write in any values you know, leaving blank what you don’t or have to find
3. Choose one of the equations that has in it what you know AND what you need
4. Solve the equation!

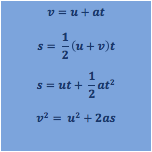These simple equations can be used to derive four equations that allow any problem involving an object moving under constant acceleration to be solved. They are given on your data sheet but it is best if you learn them:

Vertical and Horizontal Components of Velocity

· Because velocity is a vector, like force, we can take horizontal and vertical components in the same way

· Horizontal and vertical components of velocity are independent of each other

· You can use the equations of motion with the horizontal or vertical components of velocity

You are expected to deal with 2 types of problem at AS level:

Displacement-Time Graphs

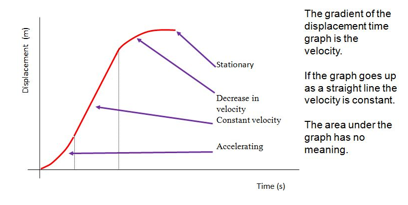
Velocity-Time Graphs

The area under the graph gives the distance travelled At any point on a curve, draw a tangent and find the gradient to calculate the acceleration at that point