A Level Physics Explained

Density

· This is a defined bulk property of a material

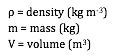
_ = density (kg m-3)
m = mass (kg)
V = volume (m3) _=m/V

· What experimental methods could you use to find density?

· Volume can be confusing e.g. how many mm3 are there in 1 m3?
Consider a box 1m x 1m x 1m:
1m = 1000mm therefore the volume in mm is:
1000 x 1000 x 1000 = 1 x 109 mm3
NOT 1000 mm3 If a material contains a mixture of materials of different densities, then the overall density can be found by:

_ = overall density (kg m-3)
V = overall volume (m3)
_A = density of material A (kg m-3)
_B = density of material B (kg m-3)
VA = volume of material A (m3)
VB = volume of material B (m3) _=(__A V_A)/V+(__B V_B)/V

Hookes Law

· The force required to stretch a spring is directly proportional to the extension

F = force applied to spring (N)
_L = extension (measured from the original length) (m)
k = spring constant (Nm-1)

· This applies as long as a spring is not stretched beyond its elastic limit

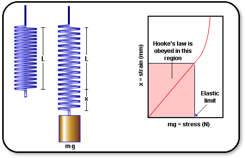· The elastic limit is the maximum force that can be applied before the spring is permanently deformed – if you take off the weights the spring will return to its original length. Any more than this and taking off the weights would leave the spring permanently stretched

The gradient in this region gives k

For 2 springs in parallel:

k_t = k₁+ k₂

For 2 springs in series:

1/k_t = (1/k₁) + (1/k₂)

E_p=1/2 F∆L=1/2 k_∆L_^2 The energy stored in the spring is the area under the graph:

Young’s Modulus

· A for a circular cross-section wire is πr2 Tensile strength applies to materials that are stretched

· Compressive strength applies to materials that are compressed

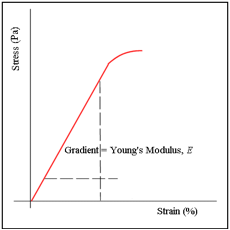
· Stress is a force per unit are a applied to a material

_ = stress (Nm-2)
T = stretching of tensile force (N)
A = cross sectional area of material (m2) _=T/A

· _=_L/L Strain is a ratio of how much a material stretches compared to its original length under load

_ = strain (no units)
_L = extension (measured from the original length) (m)
L = original length (m)

· Stiffness is a measure of how much a material will stretch when placed under stress

· Brittle materials have a high stiffness – they do not stretch much before breaking e.g. glass

· Ductile materials have a low stiffness – they stretch a lot before breaking e.g. rubber

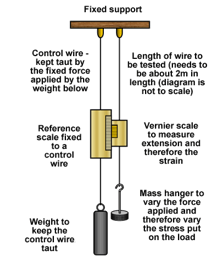To measure stiffness we use the gradient of a stress-strain graph – this is called the Young’s Modulus and is another bulk property of a material measured in units of Pascals, Pa

Stress-Strain Curves for Different Materials

Label the following points on this stress – strain graph for a metal:

· limit of proportionality

· yield point

· UTS – ultimate tensile strength

· breaking point

· region of elastic deformation

· region of plastic deformation

Draw a sketch graphs for:

· a very ductile material such as rubber

· a very brittle material such as glass

Energy Stored in a Stretched Wire

· Similar in principle to a spring – the bonds between atoms behave like springs upto the elastic limit – therefore can use the same principle to find the energy stored:

· E_p=1/2 F∆L=1/2 k_∆L_^2 The area under a Force –extension graph or:

· Loading/unloading curves or hysteresis loops show the energy converted to heat (or work done) when a material is stretched:

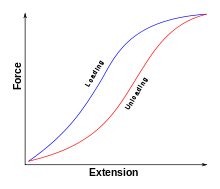
To plot a graph like this, measurements of extension need to be taken when adding weights to a material and when removing them.

After plotting a graph like this, the work done to stretch the material is the area under the loading curve.

The work done by the material in regaining its original shape is the area under the unloading curve.

The difference between the two is energy that has been converted to heat in the material.