Vectors and Scalars
· A scalar quantity has a magnitude but no direction e.g. mass
· A vector quantity has a magnitude and direction e.g. velocity
Resultant Vectors
· This is the single vector that could take the place of two (or more) other vectors. Commonly taken with velocities and forces at AS level
· Can be found using a scale drawing or mathematically
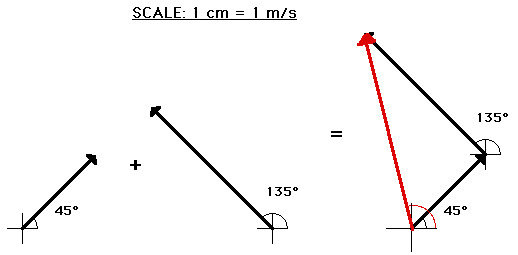
Scale Drawing
- choose a scale that will fit on your paper
- draw the two (or more vectors) end to end at the correct angles (use a protractor)
- measure the resultant length and convert to a value using your chosen scale
- measure the resultant angle with a protractor
Mathematically
-
for two forces in the same plane
choose a positive direction, in this case, right
The resultant is then the sum in that direction: 200 – 50 = 150N right
- for two forces at right angles
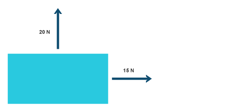
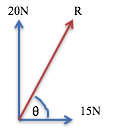
Draw a simplified diagram
 |
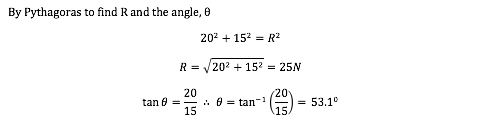Components of Vectors
· This is the opposite process to finding the resultant
· The components are a horizontal and vertical vectors that could be combined to give a resultant of the vector you have
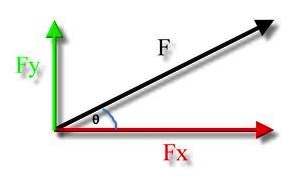The horizontal and vertical
components of the force F are FX
and FY.
(draw a triangle with the vectors and use SoCaToa if you need to)
Free Body Diagrams of Forces
· This is a simplified diagram of an object showing only the forces acting on the object as arrows in the direction the forces act
· It does not have to be to scale (unless it is to be used to find a resultant force by scale drawing) – however lines are drawn different lengths to denote the magnitude of forces. E.g. longer arrows for larger forces
· Force arrows are drawn from the point at which they act in the direction of the force
e.g. for an object in equilibria on a slope:
 |
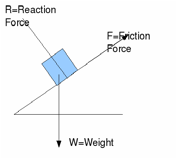Types of Forces
· Contact forces are those which arise due to the interaction of particles e.g. the support force felt by a person leaning on a desk is provided by the interaction of particles in the persons arms with the particles in the desk (complicated actually – a result of electromagnetic repulsion from the negative electrons in the arms and the table)
Friction is another common contact force
· Forces due to a field are those which arise because of a property of the object e.g. Some metals are magnetic and so feel a magnetic force – people contain very little of these materials and so do not feel it. Gravitational, Magnetic and Electric fields will be studied at A2 level
 |
Weight is a common example of this kind of force at AS level. Weight is the action of the gravitational field strength of the earth acting on a mass:
Forces in Equilibira
· Rules arise from Newtons 1st Law of Motion
“Objects remain at rest or in constant uniform motion unless acted upon by an external resultant force”
· The forces on static objects must therefore be balanced : this means a zero resultant force
· A scale diagram of the forces forms a closed shape
·
It can be usefully broken down into 2 rules for an
object in equilibria:
 |
Moments
·
 |
The moment of a force is its turning effect : this depends not only on the size of the force but also on how far away it is from the pivot point
· A moment can be in either a clockwise or anti-clockwise direction
·
The principle of moments applies to Newtons 1st
law again to situations where an object is in equilibria and has balanced
moments acting on it:
· The centre of mass of an object is the point where a single force acting at that point produces no moment.
·
 |
A couple is when there are a pair of equal forces acting in opposite directions around a pivot point.
Stability and Toppling
· An object is stable if the line of action of its weight, drawn vertically downward from its centre of mass, passes through its base
·
 |
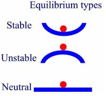A stable equilibrium is when an object is stable, then displaced from its equilibrium position will return to its original equilibrium position
· An unstable equilibrium is when it will not return to the equilibrium position