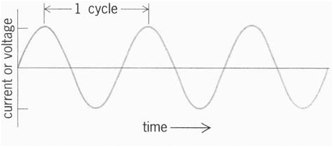
· Change direction – the electrons oscillate backwards and forwards instead of moving round the circuit
· The frequency of this oscillation for UK mains electricity is 50Hz. This means the electrons do 50 complete oscillations or cycles per second. In general:
Where:
f = frequency (Hz)
T = time period – the time for one complete cycle (s)
· Because the p.d. and current are constantly changing, it is useful to consider what the equivalent direct current would be to produce the same transfer of energy. This is called ‘rms’ current or ‘rms’ p.d.
· rms stands for root mean square and is a way of taking the average of a varying quantity
- First the quantity is squared (gets rid of negative numbers)
- Second a mean is calculated
- Third the quantity is rooted
·
At AS level you need to use the following formula
to calculate RMS values. At A2 you will need to understand rms more fully and
apply it to the velocity of particles in a gas
Where:
I0 and V0 are the peak current and p.d. respectively
·
The power delivered by a.c. is found in the same
way as with d.c.
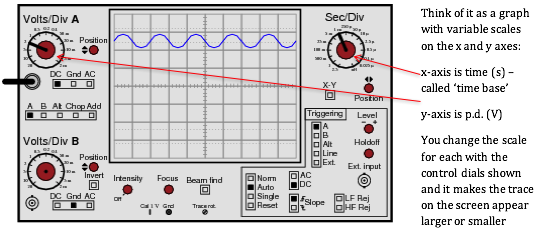
Using an
Oscilloscope (or CRO)
· to find the time period of an a.c. signal – measure the length of one complete wave on the screen in squares (called divisions or ‘div’ or sometimes in cm) then multiply that by the scale setting on the time base dial
e.g. if a wave is 2 squares long and the time base setting is 50ms/cm-1, the time period would be 2 x 50 = 100ms. This would lead to an a.c. frequency of 1/(100 x 10-3) = 10Hz
· to find the peak voltage – it is often easiest to find the ‘peak to peak’ and then divide by two – measure the height of the signal in squares and then multiply by the scale setting on the volts dial
·
It can be easier to do this if you switch the time
base off (to zero on the dial). This results in a vertical oscillating line
appearing on the screen instead of the wave:
· d.c. signals appear as horizontal lines on the screen:
