DC Circuits

Applying Kirchoffs Laws


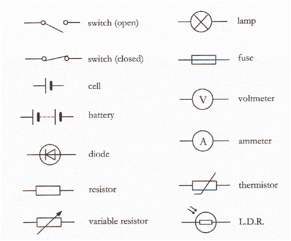
Circuit Symbols

In forward bias, when conducting, the p.d. drop across a diode is always 0.6VSome of the more common symbols used are shown. This is not exhaustive – add others….

 



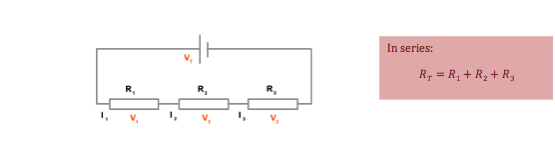
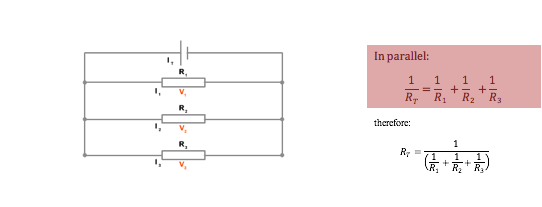
Combining Resistances

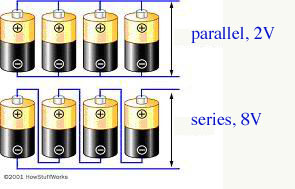
Combining Cells

Identical cells in parallel have the p.d. of each across all of them Cells in series add the p.d.

 

Circuit Rules (Kirchoffs Laws)

This section is about understanding the p.d. and current in any part of any circuit. It involves the logical application of rules and problem solving more complex circuits.

1.     The sum of the currents flowing into any junction is equal to the sum of the currents flowing out

This arises from the conservation of charge – no charge can be lost from the circuit.

Mathematically this can be written:

∑Iin = ∑Iout (at any junction)

 Important implications include:

-      Current can be measured at any point in a series circuit and give the same result

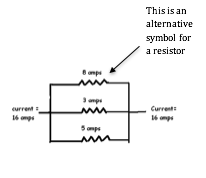
-      p.d = 6VAt a junction in a circuit, current splits in proportion to the resistance in each branch

e.g. In the diagram on the right, the current splits into proportions dependent on the resistors.

The power dissipated is also important and could be calculated using: P = IV = I2R = V2/R NB: 2 s.f. given for answers as that is max s.f. given in questionThe values of each resistor can therefore be found using :         R          =          V/I

                                                                                                                        = 6/8 = 0.8 Ω

                                                                                                                        = 6/3 = 2.0 Ω

                                                                                                                        = 6/5 = 1.2 Ω

 

2.     In any loop of a circuit, the sum of e.m.f.’s is equal to the sum of the voltage drops

∑_ = ∑V = ∑IR (in any loop)

This arises from the conservation of energy – any e.m.f. (_) provided from a cell must be lost in p.d. (V) across the components in the circuit.  Using V=IR, mathematically this becomes:

 

Important implications include:

-      P.d. is always measured by a voltmeter in parallel

-      The p.d. across different parallel branches of a circuit is always the same

-      For circuit components in series, the total p.d. is the sum of the p.d. across each branch

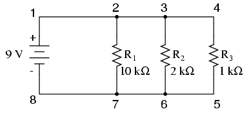
e.g. In the diagram the p.d. across each branch of the parallel circuit is 9V. Therefore the current the current flowing through each resistor is found using I         = V/R:

                                                                                                = 9/10,000 = 9.0 x 10-4A

                                                                                                = 9/2000 = 4.5 x 10-3A

                                                                                                = 9/1000 =  9.0 x 10-3A

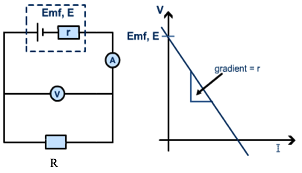
Internal Resistance

Up until now, we have thought of cells as being sources of e.m.f. with no resistance of their own. This is not true – current is impeded as it flows through a cell leading to internal resistance, r.

We consider a cell to produce an e.m.f., _ . Therefore the actual p.d. measured across the terminals of the cell must be less than this because it requires some energy for the charges to pass through the cell itself. This measured p.d. is called the terminal p.d., and the ‘lost’  p.d. depends on the internal resistance of the cell, so we think of it in terms of V=IR – in this case V=Ir as it is the internal resistance.

                        Terminal p.d. = e.m.f – p.d. ‘lost’ through internal resistance

                                    V          = _       - Ir

_ = IR + Ir or _ = I(R + r)

More usually this is written as:

Where:

_ = e.m.f. of the cell, V

I = current, A

r = internal resistance of the cell, Ω

R = external resistance in the circuit, Ω

 

Notice: Dotted line around the cell and internal resistance A graph of terminal p.d. against current gives a gradient of r and the e.m.f. as the y intercept As current increases the terminal p.d. gets decreases. More p.d. is ‘lost’ through the internal resistance The consequence of this is heating of the cell

 

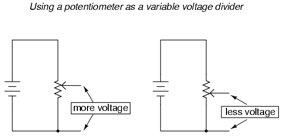
Potential Dividers

·      Converts a difference in resistance into a difference in p.d.

·      Are made using two resistors or a potentiometer

·     
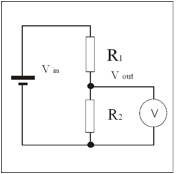
Allows a variable p.d. to be supplied from 0V to the p.d. of the cell

·      How does it work? The whole p.d. of Vin is split between R1and R2. Vout measured by the voltmeter will therefore be a proportion of Vin dependent on the values of R1and R2 Used in sensor circuits (e.g. with thermistor or L.D.R.)

Formula not on data sheet!
V_out=V_in R_2/(R_1+R_2 )
 


The potentiometer uses one variable resistor with 3 terminals to replace the two fixed resistors R1 and R2 to give the same effect. These are normally used as volume controls, dimmer switches etc.