A Level Physics Explained

Refraction

$Whenever refraction occurs, as light passes from one medium to another a small amount of the light is always reflected. This is called a partial reflection. The material light travels through is called a medium. Light rays bend toward the normal when going from a less dense to more dense materials and away from the normal when going from a more dense material to a less dense material.$

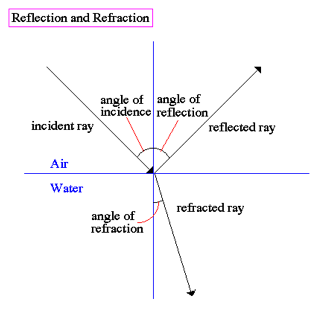
Refractive index, n is a measure of the relative speed of light in that material compared to a vacuum. A vacuum has n=1 and air, n=1.0003 (we normally take this to be 1 as well)

· It can be found using Snells Law:

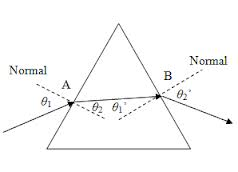
Draw diagrams with a pencil and ruler!

a generalization of this formula to deal with light moving between different materials – not just air and something else gives:

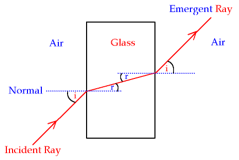
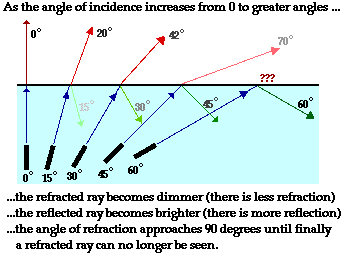
Total Internal Reflection (T.I.R.)

$When light passes from a more optically dense (higher n) material to a less optically dense (lower n) material – and the angle of incidence is higher than a certain critical angle _c – no light at all is refracted. All of it is reflected$

Optical Fibres

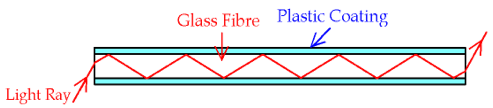
$notice refraction on entering and leaving the fibre$

· the refractive index of the glass fibre (the ‘core’) must be higher than that of the plastic coating (the ‘cladding’) for total internal reflection to occur

· This type of optical fibre is called a step-index fibre because the refractive index increases in a step from the air on the outside, to the much higher value of the cladding, to the even higher value of the core.

· The problem with step index fibres is multipath dispersion. It is possible for light to take a number of different paths through the cable so a signal sent from through will be slightly spread out.

· The solution is to make the core much narrower compared to the cladding (or to have the refractive index of the core varying gradually to a peak in the middle)

· If optical fibres touch each other, crosstalk can occur. This is where light would refract form one fibre into the next. The cladding prevents this but if e.g. water leaks into the cable this is still possible.

· Uses of optical fibres include communications and medical endoscopes

In an endoscope, bundles of fibres are used. They must be coherent – the fibres must be in the same position at each end in order for the picture to make sense.

note the two different meanings of ‘coherent’. The one below is normally what you are asked to define

Double Slit Interference (Young’s Slits)

· this experiment demonstrates the wave nature of light

· when a coherent light source is shone through an arrangement of 2 slits a distinctive pattern of light and dark fringes is observed:

Measure the fringe separation more accurately by measuring a large number and dividing by the number

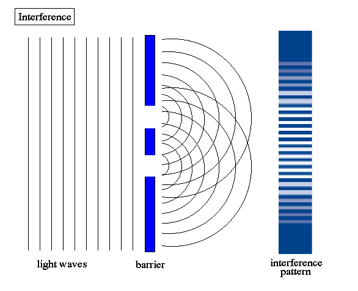the explanation for this is that the path difference for light form one slit to any point on the screen is different than for light from the other slit

· this means the light rays meet on the screen in different phases depending on the position

· where they meet in phase we observe a bright fringe, where they meet out of phase we observe a dark fringe

· constructive interference occurs at bright fringes

· destructive interference occurs at dark fringes

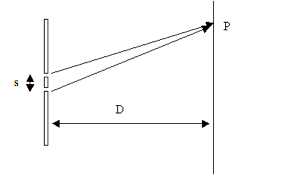
Single Slit Diffraction

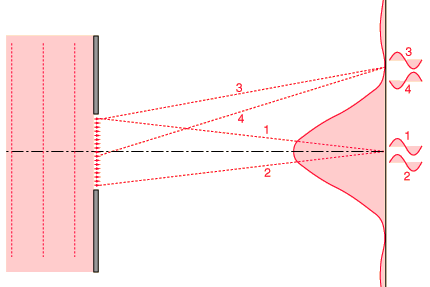
· The reason for the fringes is the same as with double slit diffraction – except now the reason for the interference is that the distance from one side of the single slit to any point on the screen is different to the distance from the other side of the slit

· The central bright fringe is twice as wide as the others which are much dimmer

Monochromatic light from a laser is used. This means single wavelength.

$With white light, the differeing amounts of diffraction depending on the wavelength can be seen – the slit is effectively splitting up the white light into its component colours$

Diffraction Gratings

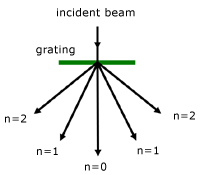
- Many slits together are called a diffraction grating

- When light diffracts through this, the bright fringes get sharper with larger dark gaps between

- Each bright fringe is called an ‘order of diffraction’ measured from 0 which is the centre

- The difference between using monochromatic and white light can be seen below:


	$Question Tips If you get a decimal for the order of diffraction always round down to the nearest whole number To find the maximum order of diffraction use 900 for the angle$

If there are 500 slits per mm – to find d:
500 slits per mm = 500 x 1000 = 5 x 105 slits per metre
1/5 x 105 = 2 x 10-6m

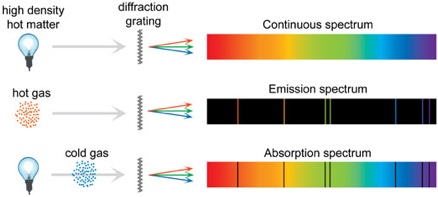
Spectra

· Diffraction gratings are used in spectrometers to produce spectra because they diffract the light by different angles depending on its wavelength

Optics